
In this report, we describe research undertaken by Jonathon Wanley (undergraduate Mathematics student, currently between 2nd and 3rd year) during his eight-week summer project with Dr Robin Thompson (Fellow in Applied Mathematics).
Background and aims
During infectious disease outbreaks, isolation of detected infected individuals is a common non-pharmaceutical intervention (NPI) implemented to limit the spread of infection. By reducing the number of contacts between infectious and susceptible individuals, transmissions are prevented, thereby reducing the magnitude of the outbreak. For example, during the COVID-19 pandemic, individuals who suspected they were infected (e.g., because they developed relevant symptoms) or tested positive for infection were required to self-isolate.
Mathematical models are commonly used to test different control interventions during outbreaks. Models were used during the COVID-19 pandemic to guide both NPIs [1] and decisions regarding vaccine deployment [2]. In this summer project, we considered the use of models to assess the efficacy of isolation strategies. Specifically, we: i) developed a mathematical model for estimating the risk, when a pathogen first arrives in a host population, that a major outbreak will follow (as opposed to the outbreak fading out with few cases); ii) used the model to test the effectiveness of isolation at reducing the risk of a major outbreak. While we used COVID-19 as a motivating case-study, in principle our general approach could be used to explore the effectiveness of isolation at mitigating transmission of a range of pathogens.
Our main finding was that similar isolation strategies can be predicted to have different effects on the probability of a major outbreak, depending on how isolation is implemented in the mathematical model. In particular, for a fixed overall reduction in the number of contacts prevented by isolation (termed “isolation effectiveness” by policy-makers), it is important to understand whether contacts are reduced in a “leaky” or “all or nothing” fashion (about which more details below). This demonstrates that mathematicians must consider the assumptions underlying models of isolation and other interventions carefully when determining the impacts of infectious disease control strategies.
Modelling approach and results
In the epidemiological model that we developed, we assumed that two possible event types could occur – infection and removal. Infections occur when susceptible individuals come into contact with infected individuals, leading to the transmission of the pathogen. Removal involves individuals either recovering or being otherwise removed from the population (e.g., dying). The interplay between these events is pivotal in any outbreak’s progression. The ratio of the infection rate to the removal rate is termed the basic reproduction number, R0, which describes the mean number of infections generated by a single infected individual who is introduced into an otherwise entirely susceptible host population.
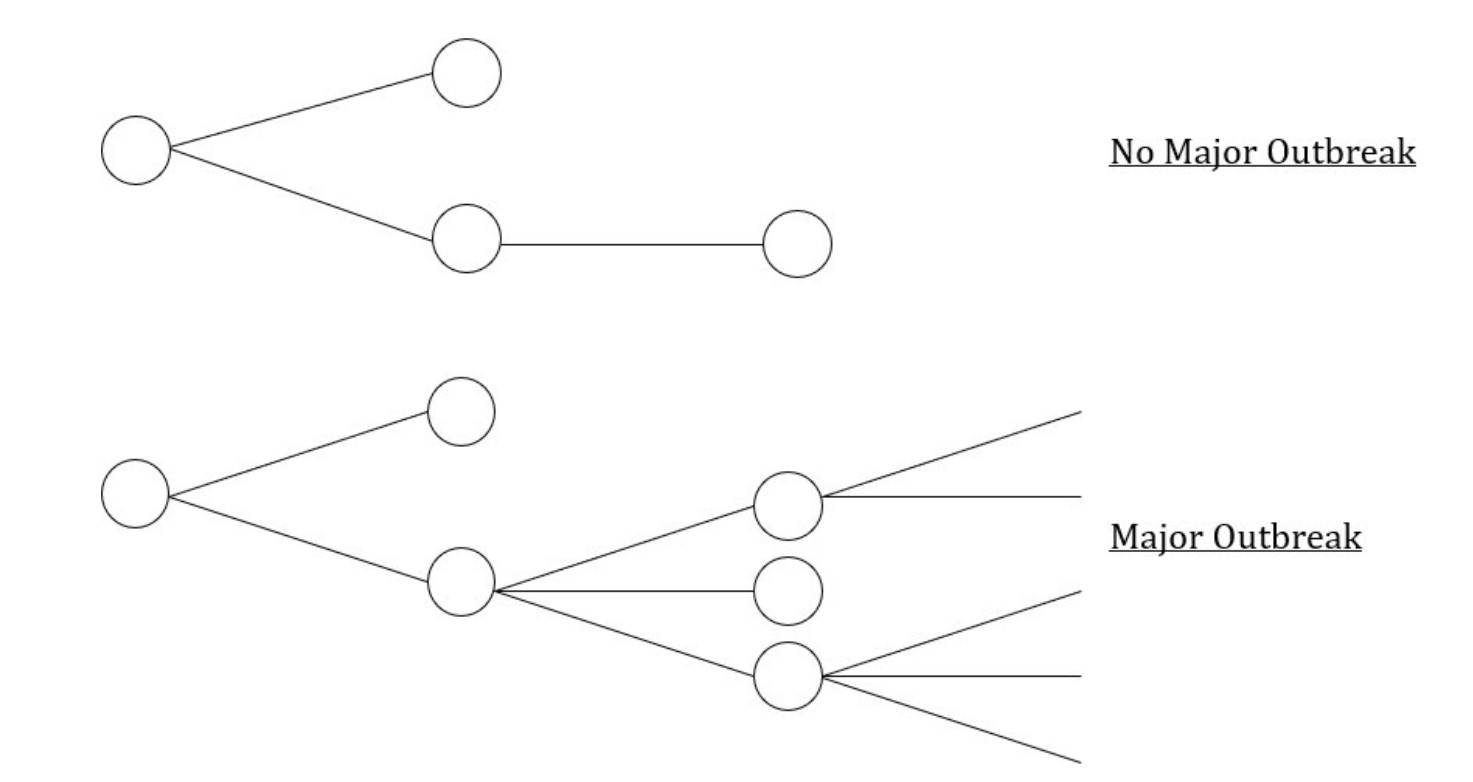
To assess the probability of a major outbreak, we focussed on the early stages of an outbreak, in which pathogens either fade out after infecting only a small number of individuals (Figure 1 – top panel) or become widespread, affecting a substantial proportion of the population (Figure 1 – bottom panel). We adapted a previous modelling approach for estimating the probability of a major outbreak [3] and developed a transmission model that accounts for individual host-level changes in infectiousness during infection and isolation of detected infected individuals.
Inspired by related concepts in vaccination modelling (see e.g. [4]), we considered two different approaches for modelling isolation, both corresponding to a fixed overall reduction in the number of contacts between individuals in the host population:
Leaky isolation. All infected individuals in the population are isolated, but with imperfect effectiveness (i.e., isolated individuals still generate some infections).
All-or-nothing isolation. Only some infected individuals are isolated, but are isolated perfectly (i.e., infected individuals do not generate any infections while isolated).
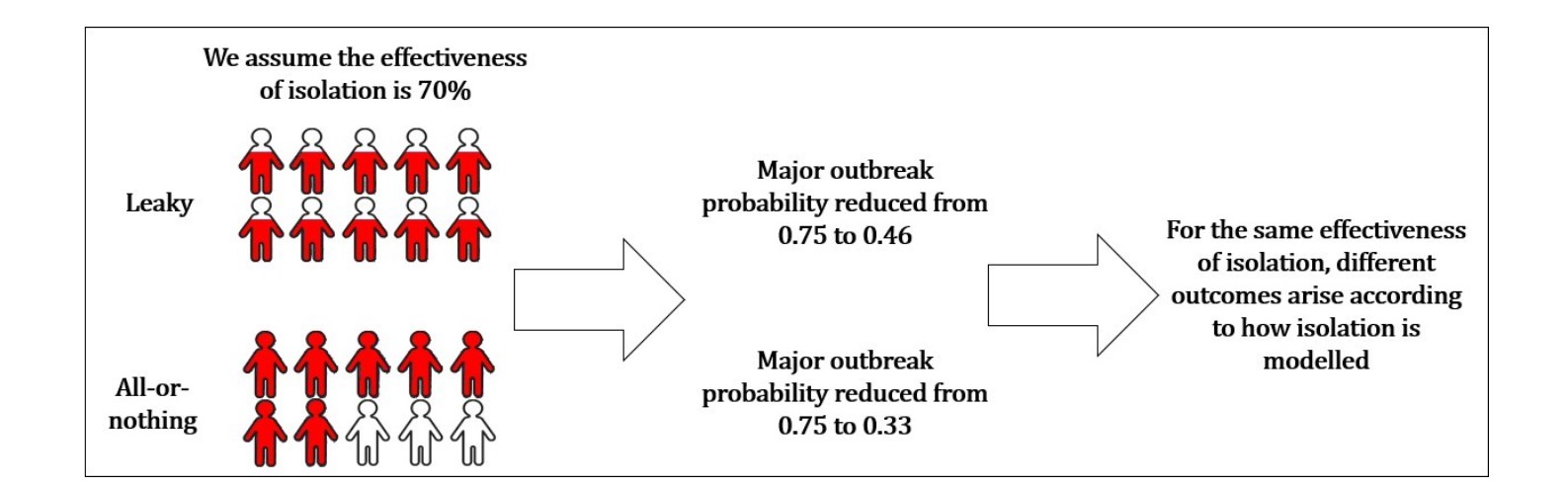
We denoted the proportion of the population who isolate by λ, and the reduction in the number of contacts that an isolating individual has by μ. Hence, the overall reduction in contacts in the population is determined by the product λμ.
As an example, a leaky isolation strategy in which all individuals are isolated and isolating individuals have 70% fewer contacts would correspond to an overall reduction in contacts in the population of λμ = 1 × 0.7 = 0.7. Similarly, an all-or-nothing isolation strategy in which 70% of individuals are isolated would correspond to an overall reduction in contacts in the population of λμ = 0.7 × 1 = 0.7. In both scenarios, the overall effectiveness of isolation in terms of reducing contacts might be deemed to be 70%, however – as we showed in the project and explain below – these scenarios can correspond to different risks of large outbreaks occurring (Figure 2).
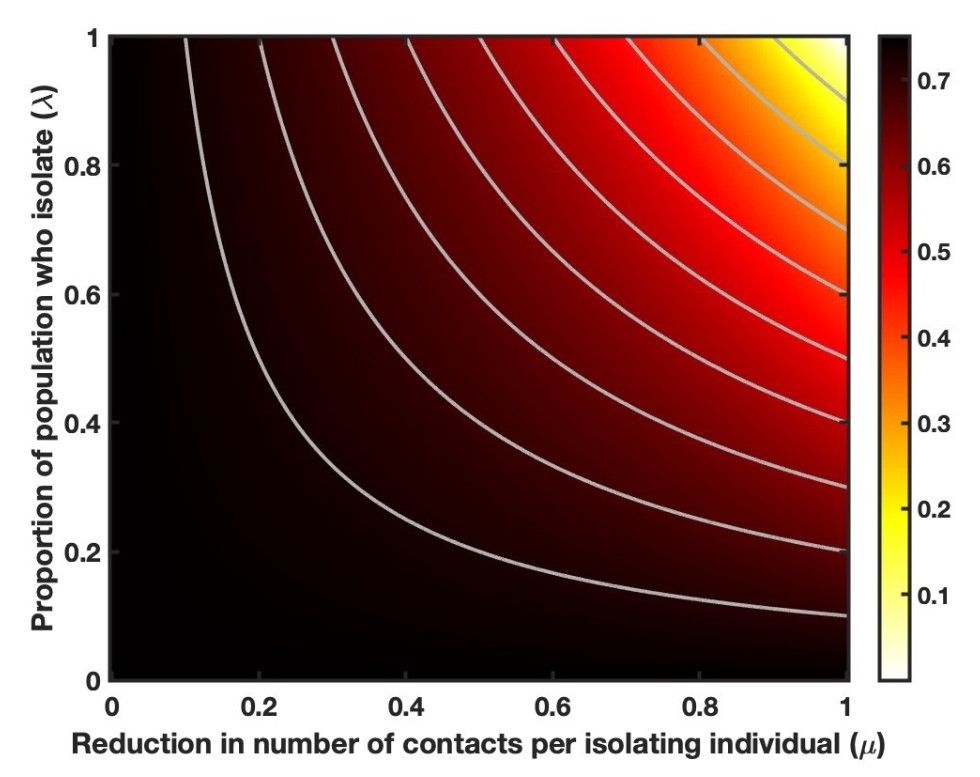
Results considering a range of values of λ and μ are shown in Figure 3.
Conclusions
To identify the optimal intervention strategy to implement during an infectious disease outbreak, policy-makers require accurate estimates of the efficacies of different public health measures. In this project, we adapted mathematical approaches commonly used for modelling the impacts of vaccination to consider the effects of isolation on outbreak risks. We compared the probability of a major outbreak under so-called “leaky” isolation to the analogous quantity under “all-or-nothing” isolation, showing that the assumed mode by which contacts are reduced in the host population affects estimates of the probability of a major outbreak. The key reason for this result is that, when determining the probability of a major outbreak, the characteristics of the individuals infected early in the outbreak are essential in shaping the risk of a large outbreak developing. In a scenario with leaky isolation, the first infected individual will isolate imperfectly. In contrast, in a scenario with all-or-nothing isolation, the first infected individual may isolate perfectly, leading to a lower (or equal) chance of a large outbreak following.
In addition to the results presented here, we conducted a range of other analyses, corresponding to different values of R0, varying adherence to isolation between infected individuals and the addition of further complexity in the underlying transmission model. In each scenario considered, our overall qualitative conclusion remained unchanged: for a fixed reduction in contacts due to isolation, how isolation is implemented in the model affected the probability of a major outbreak.
Going forwards, additional epidemiological detail could be added to the modelling approach. This could include, for example, consideration of heterogeneity in transmissibility between infected individuals to account for the presence of “super- spreaders” [5], or the inclusion of realistic infectious period distributions [6,7]. Further work on this epidemiological modelling framework will enable outbreak risks under different isolation strategies to be estimated more precisely to aid public health policy-making.
References
- Thompson RN. Epidemiological models are important tools for guiding COVID-19 interventions. BMC Med. 2020;18: 152.
- Moore S, Hill EM, Dyson L, Tildesley MJ, Keeling MJ. Modelling optimal vaccination strategy for SARS-CoV-2 in the UK. PLOS Comput Biol. 2021;17: e1008849.
- Southall E, Ogi-Gittins Z, Kaye AR, Hart WS, Lovell-Read FA, Thompson RN. A practical guide to mathematical methods for estimating infectious disease outbreak risks. J Theor Biol. 2023;562: 111417.
- Shim E, Galvani AP. Distinguishing vaccine efXicacy and effectiveness. Vaccine. 2012;30: 6700–6705.
Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438: 355–359. - Wearing HJ, Rohani P, Keeling MJ. Appropriate models for the management of infectious diseases. PLoS Med. 2005;2: 0621–0627.
- Lloyd AL. Realistic distributions of infectious periods in epidemic models: Changing patterns of persistence and dynamics. Theor Pop Biol. 2001;60: 59–71.
Acknowledgements
The authors would like to thank St Hilda's College, University of Oxford, for the funding that enabled this undergraduate summer research project to be undertaken.